
Pythagoras fra Samos (582 f.Kr. – 507 f.Kr.) var en græsk filosof, mystiker, matematiker, musikteoretiker og musikterapeut. © svaan.dk Pythagoras forenede i sin lære matematik og talmystik med musik (både udøvelse og teori) og forestillingen om sjælens udødelighed. Pythagoras har lagt navn til den pythagoræiske læresætning, men han opfandt den ikke, da den var kendt i Babylon allerede ca 1800 f.Kr.
Pythagoras sætning angår forholdet mellem længden af siderne i en retvinklet trekant.
Den lyder: Summen af kateternes kvadrater, i en retvinklet trekant, er lig med kvadratet på hypotenusen. I symbolsk notation: a² + b² = c² En af Pythagoras’ studenter, Hippasos fra Metapontum, grundede over kvadratroden af 2.
Han kom ikke frem til nogen brøk, men til et irrationelt tal.

Pythagoras forklarede verden ud fra hele tal og så Hippasos’ påstand som et kætteri. Studenten blev derfor smidt i havet af andre pythagoreere og druknede.
Pythagoras giftede sig med en af sine yndlingselever, Theano.Leder for den syriske nyplatoniske skole på Evboia, Jamblikos, skrev flere bøger om pythagoréerne, deriblandt at Theano arbejdede med det gyldne snit.
Ansvaret for Pythagoras’ efterladte skrifter gik til deres datter Damo; de to andre døtre, Arignote og Miyia, skal også have været pythagoréere. Af gamle medlemslister fremgår, at ca syv procent af medlemmerne var kvinder.Den pythagoræiske læresætning beskriver forholdet mellem sidelængderne i en retvinklet trekant. Det er en af de grundlæggende sætninger i den euklidiske geometri. Den siger, at i alle retvinklede trekanter er summen af kateternes kvadrat lig hypotenusens kvadrat. Sætningen kan også udtrykkes som ligning, idet kateternes længder benævnes og og hypotenusens benævnes , ligesom på illustrationen: Det er derfor muligt at beregne en sidelængde i en retvinklet trekant, når de to andre sidelængder er kendte.
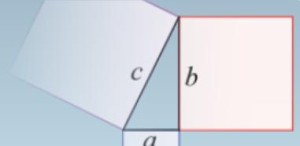
Fx findes hypotenusen ved at tage kvadratroden af summen af og s kvadrater, altså Læresætningen er fejlagtigt opkaldt efter Pythagoras da han var den første til at udbrede den, ikke opdage den. Sæt af heltalige løsninger til den pythagoræiske læresætning kaldes pythagoræiske tal.
